Ex 5.1 Class 9 Maths
Question 1.
Which of the following statements are true and which are false? Give reasons for your answers.
(i) Only one line can pass through a single point.
(ii) There are an infinite number of lines which pass through two distinct points.
(iii) A terminated line can be produced indefinitely on both the sides.
(iv) If two circles are equal, then their radii are equal.
(v) In figure, if AB – PQ and PQ = XY, then AB = XY.

Solution:
(i) False
Reason : If we mark a point O on the surface of a paper. Using pencil and scale, we can draw infinite number of straight lines passing
through O.
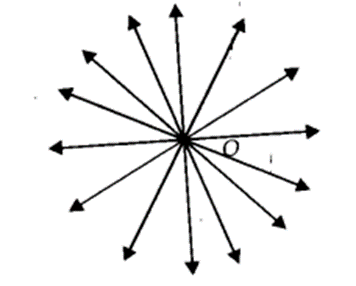
(ii) False
Reason : In the following figure, there are many straight lines passing through P. There are many lines, passing through Q. But there is one and only one line which is passing through P as well as Q.
(iii) True
Reason: The postulate 2 says that “A terminated line can be produced indefinitely.”
(iv) True
Reason : Superimposing the region of one circle on the other, we find them coinciding. So, their centres and boundaries coincide.
Thus, their radii will coincide or equal.
(v) True
Reason : According to Euclid’s axiom, things which are equal to the same thing are equal to one another.
Question 2.
Give a definition for each of the following terms. Are there other terms that need to be defined first? What are they and how might you define them?
(i) Parallel lines
(ii) Perpendicular lines
(iii) Line segment
(iv) Radius of a circle
(v) Square
Solution:
Yes, we need to have an idea about the terms like point, line, ray, angle, plane, circle and quadrilateral, etc. before defining the required terms.
Definitions of the required terms are given below: (i) Parallel Lines:
Two lines l and m in a plane are said to be parallel, if they have no common point and we write them as l ॥ m.

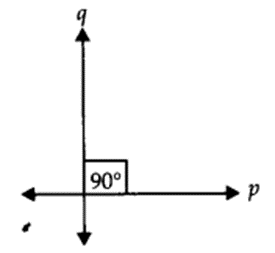
(ii) Perpendicular Lines:
Two lines p and q lying in the same plane are said to be perpendicular if they form a right angle and we write them as p ⊥ q.
(iii) Line Segment:
A line segment is a part of line and having a definite length. It has two end-points. In the figure, a line segment is shown having end points A and B. It is written as AB¯¯¯¯¯¯¯¯ or BA¯¯¯¯¯¯¯¯.

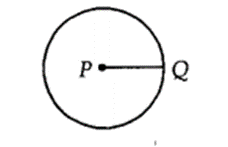
(iv) Radius of a circle :
The distance from the centre to a point on the circle is called the radius of the circle. In the figure, P is centre and Q is a point on the circle, then PQ is the radius.
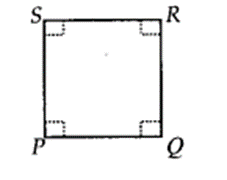
(v) Square :
A quadrilateral in which all the four angles are right angles and all the four sides are equal is called a square. Given figure, PQRS is a square.
Ex 5.1 Class 9 Maths
Question 3.
Consider two ‘postulates’ given below
(i) Given any two distinct points A and B, there exists a third point C which is in between A and B.
(ii) There exist atleast three points that are not on the same line.
Do these postulates contain any undefined terms? Are these postulates consistent? Do they follow from Euclid’s postulates? Explain.
Solution:
Yes, these postulates contain undefined terms such as ‘Point and Line’. Also, these postulates are consistent because they deal with two different situations as
(i) says that given two points A and B, there is a point C lying on the line in between them. Whereas
(ii) says that, given points A and B, you can take point C not lying on the line through A and B.
No, these postulates do not follow from Euclid’s postulates, however they follow from the axiom, “Given two distinct points, there is a unique line that passes through them.” Ex 5.1 Class 9 Maths
Question 4.
If a point C lies between two points A and B such that AC = BC, then prove that AC = 12 AB, explain by drawing the figure.
Solution:
We have,
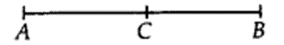
AC = BC [Given]
∴ AC + AC = BC + AC
[If equals added to equals then wholes are equal]
or 2AC = AB [∵ AC + BC = AB]
or AC = 12AB
Ex 5.1 Class 9 Maths
Question 5.
In question 4, point C is called a mid-point of line segment AB. Prove that every line segment has one and only one mid-point.
Solution:
Let the given line AB is having two mid points ‘C’ and ‘D’.
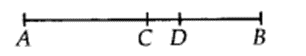
AC = 12AB ……(i)
and AD = 12AB ……(ii)
Subtracting (i) from (ii), we have
AD – AC = 12AB−12AB
or AD – AC = 0 or CD = 0
∴ C and D coincide.
Thus, every line segment has one and only one mid-point.
Ex 5.1 Class 9 Maths
Question 6.
In figure, if AC = BD, then prove that AB = CD.
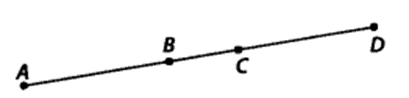
Solution:
Given: AC = BD
⇒ AB + BC = BC + CD
Subtracting BC from both sides, we get
AB + BC – BC = BC + CD – BC
[When equals are subtracted from equals, remainders are equal]
⇒ AB = CD
Ex 5.1 Class 9 Maths
Question 7.
Why is axiom 5, in the list of Euclid’s axioms, considered a ‘universal truth’? (Note that, the question is not about the fifth postulate.)
Solution:
As statement is true in all the situations. Hence, it is considered a ‘universal truth.’
Ex 5.2 Class 9 Maths
Question 1.
How would you rewrite Euclid’s fifth postulate so that it would be easier to understand?
Solution:
We can write Euclid’s fifth postulate as ‘Two distinct intersecting lines cannot be parallel to the same line.’ Ex 5.2 Class 9 Maths
Question 2.
Does Euclid’s fifth postulate imply the existence of parallel lines ? Explain.
Solution:
Yes. If a straight line l falls on two lines m and n such that sum of the interior angles on one side of l is two right angles, then by Euclid’s fifth postulate, lines m and n will not meet on this side of l. Also, we know that the sum of the interior angles on the other side of the line l will be two right angles too. Thus, they will not meet on the other side also.
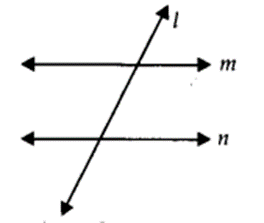
∴ The lines m and n never meet, i.e, They are parallel.
Question 1: What are the five postulates of Euclid’s Geometry?
Answer 1: Euclid’s postulates are:
- A straight line may be drawn from one point to any other point.
- A required terminated line can be produced indefinitely.
- A required circle can be drawn with any centre and radius.
- All right angles are equal.
- Suppose a given straight line intersects on two straight lines making the interior angles on the exact side of it brought together less than two right angles. In that case, the two straight lines, if produced indefinitely, meet on that side on which the sum of the given angles is less than two right angles.
Question 2: Which of the given following assertions are true and which are false? Give explanations for your solutions.
(i) Just one line can pass through a given single point.
(ii) An infinite number of lines pass through two required distinct points.
(iii) A given terminated line can be created indefinitely on both sides.
(iv) If two circles are equal, their radii are equal.
(v) In the figure alongside , if AB = PQ and PQ = XY, then AB = XY.
Answer 2:
(i) The above statement is False
Reason: If we draw a point O on the surface of a paper. U
tilising pencil and scale, we can draw an infinite number of straight lines passing
through O.
Question 3: Describe parallel lines. Are there other representations that need to be specified first? What are they, and how might you express them?
Answer 3:The required two coplanar lines in a plane not intersecting are also said to be parallel lines. The other term intersecting, is undefined.
Question 4: Define the following terms individually. Are there other terms that ought to be specified first? What are they, and how will you describe them?
(i)The parallel lines
(ii) The perpendicular lines
(iii) The line segment
(iv) The radius of a circle
(v) The square
Answer 4: Yes, we need to know the words like point, line, ray, angle, plane, circle and quadrilateral, etc., before describing the necessary words.
Descriptions of the necessary words are given below:
(i) The parallel lines:
The two lines l and m in a plane are expressed as parallel if they have no common point, and we note them as l ॥ m.
The distance between the lines always remains the same.
Lines l and m are parallel on a plane surface.
(ii) The perpendicular lines:
The two lines, p and q, lying in the same plane, are expressed to be perpendicular if they intersect each other at right angle, and we note them as p ⊥ q. Lines q and p are perpendicular to each other
(iii)The line Segment:
A required line segment is a part of a line and has a definite length. It has two endpoints. In the figure, a line segment has endpoints A and B. It cannot be extended. It is written as
AB or BA
(iv) The radius of a circle :
The length from the centre to a point on the circle is called the radius of the circle. Radius helps in calculation of diameter, circumference and area.In the figure alongside, P is the centre, Q is a point on the circle, and PQ is the radius.
(v) Square :
A quadrilateral in which all the four angles are right angles and all the four sides are equal is called a square. Opposite sides of the square are parallel. Two diagonals bisect each other at a right angle. Given the figure, PQRS is a square.
Question 5: Define perpendicular lines. Are there other words that need to be described first? What are they, and how may you define them?
Answer 5:The two coplanar (in a plane) lines are perpendicular if the required angle between them at the given point of intersection is one right angle. In other words, the point of intersection and one right angle are undefined.
Question 6: In figure alongside, if AC = BD, then prove that AB = CD.
Answer 6: Given: AC = BD
⇒ AB + BC = BC + CD
Subtracting BC from both sides, we get
AB + BC – BC = BC + CD – BC
[When the equivalents are subtracted from equals, remainders are equal]
⇒ AB = CD
Question 7: Define the line segment. Are there other terms that ought to be defined first? What are they, and how will you define them?
Answer 7:A line segment PQ of a line ‘l is the continuous part of line I with endpoints P and Q.
Here, the continuous part of the line ‘l is undefined.
Question 8: Does Euclid’s fifth postulate imply the existence of parallel lines? Explain.
Answer 8: Yes. If a required straight line l falls on two lines m and n such that the sum of the given interior angles on one side of l is two right angles, then by Euclid’s fifth postulate, the lines m and n will not meet on this side of l. Furthermore, we understand that the sum of the given interior angles on the other side of the line l will be the two given right angles too. Hence, they will not meet on the other side also.
∴ The lines m and n never meet; they are parallel. In figure, if AC = BD, then verify that AB = CD.
Question 9: Solve the required equation a – 15 = 25 and state which axiom you use here.
Answer 9: a – 15 = 25
By adding 15 to both sides, we obtain
a – 15 + 15 = 25 + 15 [using Euclid’s second axiom]
a = 40
Question 10: Assume the two ‘postulates’ given below
(i) Given any two distinct points, A and B, there exists a third point, C, between A and B.
(ii) At least three points are not on the same line.
Do these postulates contain any undefined terms? Are these postulates consistent? Do they follow Euclid’s postulates? Explain.
Answer 10: Yes, these postulates have undefined terms such as ‘Point and Line. Furthermore, these postulates are consistent because they deal with two different situations as
(i) states that required two points A and B, there is a point C on the line between them. Whereas
(ii) states that, given points A and B, you can take point C, not lying on the line through points A and B.
No, these postulates do not obey Euclid’s postulates. Nevertheless, they abide by the axiom, “Given two distinct points, there is a unique line that passes through them.”
Question 11: Ram and Ravi have the exact weight. If they ever gain weight by 2 kg, how will their new weights be compared?
Answer 11: Let x kg be the weight of each of Ram and Ravi.
On adding 2 kg,
The weight of Ram and Ravi will be (x + 2) kg each.
According to Euclid’s second axiom, the wholes are equal when equals are added to equals.
So, the weight of Ram and Ravi are equal.
Question 12: In question 4, point C is called a mid-point line segment AB. Verify that every line segment has one and only one mid-point.
Answer 12: Let the given line AB have two midpoints,’ C’ and ‘D’.
AC = 1/2AB ……(i)
and AD = 1/2AB ……(ii)
Subtracting (i) from (ii), we have
AD – AC = 1/2AB−1/2AB
or AD – AC = 0 or CD = 0
∴ C and D coincide.
Therefore, each line segment has one and only one mid-point.
Question 13: If point C be the mid-point of a line segment AB, then write the relation among AC, BC and AB.
Answer 13: Here, C is the mid-point of AB
AC = BC
AC = BC = 1/2AB
Question 14: Read the required statements:
A given equilateral triangle is a polygon made up of three line segments, of which two line segments are equivalent to the third one, and all its angles are 60° each.
Explain the words used in this description that you feel are essential. Are there any indefinite words in this? Can you explain that all sides and all angles are equivalent in an equilateral triangle?
Answer 14: The terms that need to be defined are
(i) The given polygon A closed figure bounded by three or more line segments.
(ii) The given line segment is part of a line with two endpoints.
(iii) The given line Undefined term.
(iv) The given point Undefined term.
(v) Angle =A given figure formed by two rays with one common initial point.
(vi) Acute angle =Angle whose measure is from 0° to 90°.
Here undefined terms are line and point.
All the angles of any given equilateral triangle are 60° each (given).
The two line segments are equal to the third one (given).
Hence, all three sides of an equilateral triangle are equal because, according to Euclid’s axiom, things equal to the same thing are equal.
Download Mennta App and get access to free video lectures and hand crafted notes.