Class 9 Maths Chapter 10 Circles
Ex 10.1 Class 9 Maths Question 1.
Fill in the blanks.
(i) The centre of a circle lies in ___ of the circle. (exterior/interior)
(ii) A point, whose distance from the centre of a circle is greater than its radius lies in ____ of the circle, (exterior/interior)
(iii) The longest chord of a circle is a ____ of the circle.
(iv) An arc is a ____ when its ends are the ends of a diameter.
(v) Segment of a circle is the region between an arc and ____ of the circle.
(vi) A circle divides the plane, on which it lies, in ____ parts.
Solution:
(i) interior
(ii) exterior
(iii) diameter
(iv) semicircle
(v) the chord
(vi) three
Ex 10.1 Class 9 Maths Question 2.
Write True or False. Give reason for your answers.
(i) Line segment joining the centre to any point on the circle is a , radius of the circle.
(ii) A circle has only finite number of equal chords.
(iii) If a circle is divided into three equal arcs, each is a major arc.
(iv) A chord of a circle, which is twice as long as its radius, is a diameter of the circle.
(v) Sector is the region between the chord and its corresponding arc.
(vi) A circle is a plane figure.
Solution:
(i) True [∵ All points on the circle are equidistant from the centre]
(ii) False [ ∵ A circle can have an infinite number of equal chords]
(iii) False [∵ Each part will be less than a semicircle]
(iv) True [ ∵ Diameter = 2 x Radius]
(v) False [ ∵ The region between the chord and its corresponding arc is a segment]
(vi) True [ ∵ A circle is drawn on a plane]
Ex 10.1 Ex 10.2 Class 9 Maths Question 1.
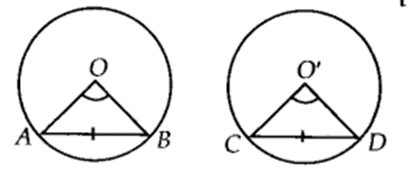
Recall that two circles are congruent, if they have the same radii. Prove that equal chords of congruent circles subtend equal angles at their centres
Solution:
Given: Two congruent circles with centres O and O’ and radii r, which have chords AB and CD respectively such that AB = CD.
To Prove: ∠AOB = ∠CO’D
Proof: In ∆AOB and ∆CO’D, we have
AB = CD [Given]
OA = O’C [Each equal to r]
OB = O’D [Each equal to r]
∴ ∆AOB ≅ ∆CO’D [By SSS congruence criteria]
⇒ ∠AOB = ∠CO’D [C.P.C.T.]
Ex 10.2 Class 9 Maths Question 2.
Prove that, if chords of congruent circles subtend equal angles at their centres, then the chords are equal.
Solution:
Given: Two congruent circles with centres O & O’ and radii r which have chords AB and CD respectively such that ∠AOB = ∠CO’D.
To Prove: AB = CD
Proof: In ∆AOB and ∆CO’D, we have
OA = O’C [Each equal to r]
OB = O’D [Each equal to r]
∠AOB = ∠CO’D [Given]
∴ ∆AOB ≅ ∆CO’D [By SAS congruence criteria]
Hence, AB = CD [C.P.C.T.]
Ex 10.3 Class 9 Maths Question 1.
Draw different pairs of circles. How many points does each pair have in common? What is the maximum number of common points?
Solution:
Let us draw different pairs of circles as shown below:
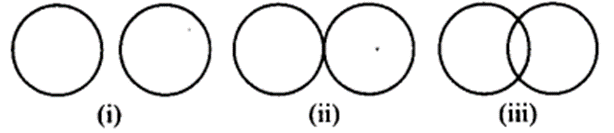
We have
| Figure | Maximum number of common points |
| (i) | nil |
| (ii) | one |
| («i) | two |
Thus, two circles can have at the most two points in common.
Ex 10.3 Class 9 Maths Question 2.
Suppose you are given a circle. Give a construction to find its centre.
Solution:
Steps of construction :
Step I : Take any three points on the given circle. Let these points be A, B and C.
Step II : Join AB and BC.
Step III : Draw the perpendicular bisector, PQ of AB.
Step IV: Draw the perpendicular bisector, RS of BC such that it intersects PQ at O.
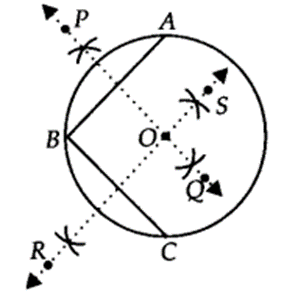
Thus, ‘O’ is the required centre of the given drcle.
Ex 10.3 Class 9 Maths Question 3.
If two circles intersect at two points, prove that their centres lie on the perpendicular bisector of the common chord.
Solution:
We have two circles with centres O and O’, intersecting at A and B.
∴ AB is the common chord of two circles and OO’ is the line segment joining their centres.
Let OO’ and AB intersect each other at M.
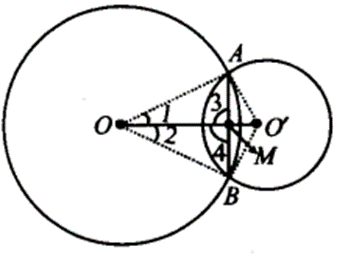
∴ To prove that OO’ is the perpendicular bisector of AB,
we join OA, OB, O’A and O’B. Now, in ∆QAO’ and ∆OBO’,
we have
OA = OB [Radii of the same circle]
O’A = O’B [Radii of the same circle]
OO’ = OO’ [Common]
∴ ∆OAO’ ≅ ∆OBO’ [By SSS congruence criteria]
⇒ ∠1 = ∠2 , [C.P.C.T.]
Now, in ∆AOM and ∆BOM, we have
OA = OB [Radii of the same circle]
OM = OM [Common]
∠1 = ∠2 [Proved above]
∴ ∆AOM = ∆BOM [By SAS congruence criteria]
⇒ ∠3 = ∠4 [C.P.C.T.]
But ∠3 + ∠4 = 180° [Linear pair]
∴∠3=∠4 = 90°
⇒ AM ⊥ OO’
Also, AM = BM [C.P.C.T.]
⇒ M is the mid-point of AB.
Thus, OO’ is the perpendicular bisector of AB.
Ex 10.4 Class 9 Maths Question 1.
Two circles of radii 5 cm and 3 cm intersect at two points and the distance between their centres is 4 cm. Find the length of the common chord.
Solution:
We have two intersecting circles with centres at O and O’ respectively. Let PQ be the common chord.
∵ In two intersecting circles, the line joining their centres is perpendicular bisector of the common chord.
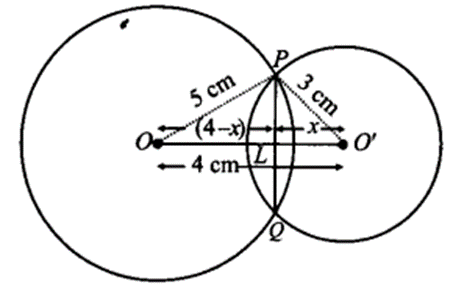
∴∠OLP = ∠OLQ = 90° and PL = LQ
Now, in right ∆OLP, we have
PL2 + OL2 = 2
⇒ PL2 + (4 – x)2 = 52
⇒ PL2 = 52 – (4 – x)2
⇒ PL2 = 25 -16 – x2 + 8x
⇒ PL2 = 9 – x2 + 8x …(i)
Again, in right ∆O’LP,
PL2 = PO‘2 – LO‘2
= 32 – x2 = 9 – x2 …(ii)
From (i) and (ii), we have
9 – x2 + 8x = 9 – x2
⇒ 8x = 0
⇒ x = 0
⇒ L and O’ coincide.
∴ PQ is a diameter of the smaller circle.
⇒ PL = 3 cm
But PL = LQ
∴ LQ = 3 cm
∴ PQ = PL + LQ = 3cm + 3cm = 6cm
Thus, the required length of the common chord = 6 cm.
Ex 10.4 Class 9 Maths Question 2.
If two equal chords of a circle intersect within the circle, prove that the segments of one chord are equal to corresponding segments of the other chord.
Solution:
Given: A circle with centre O and equal chords AB and CD intersect at E.
To Prove: AE = DE and CE = BE
Construction : Draw OM ⊥ AB and ON ⊥ CD.
Join OE.
Proof: Since AB = CD [Given]
∴ OM = ON [Equal chords are equidistant from the centre]
Now, in ∆OME and ∆ONE, we have
∠OME = ∠ONE [Each equal to 90°]
OM = ON [Proved above]
OE = OE [Common hypotenuse]
∴ ∆OME ≅ ∆ONE [By RHS congruence criteria]
⇒ ME = NE [C.P.C.T.]
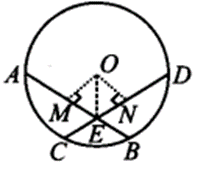
Adding AM on both sides, we get
⇒ AM + ME = AM + NE
⇒ AE = DN + NE = DE
∵ AB = CD ⇒ 12AB = 12DC
⇒ AM = DN
⇒ AE = DE …(i)
Now, AB – AE = CD – DE
⇒ BE = CE …….(ii)
From (i) and (ii), we have
AE = DE and CE = BE
Ex 10.4 Class 9 Maths Question 3.
If two equal chords of a circle intersect within the circle, prove that the line joining the point of intersection to the centre makes equal angles with the chords.
Solution:
Given: A circle with centre O and equal chords AB and CD are intersecting at E.
To Prove : ∠OEA = ∠OED
Construction: Draw OM ⊥ AB and ON ⊥ CD.
Join OE.
Proof: In ∆OME and ∆ONE,
OM = ON
[Equal chords are equidistant from the centre]
OE = OE [Common hypotenuse]
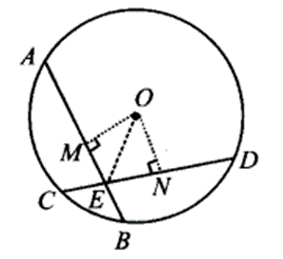
∠OME = ∠ONE [Each equal to 90°]
∴ ∆OME ≅ ∆ONE [By RHS congruence criteria]
⇒ ∠OEM = ∠OEN [C.P.C.T.]
⇒ ∠OEA = ∠OED
Ex 10.4 Class 9 Maths Question 4.
If a line intersects two concentric circles (circles with the same centre) with centre 0 at A, B, C and D, prove that AB = CD (see figure).
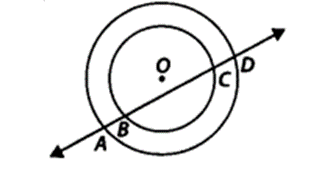
Solution:
Given : Two circles with the common centre O.
A line D intersects the outer circle at A and D and the inner circle at B and C.
To Prove : AB = CD.
Construction:
Draw OM ⊥ l.
Proof: For the outer circle,
OM ⊥ l [By construction]
∴ AM = MD …(i)
[Perpendicular from the centre to the chord bisects the chord]
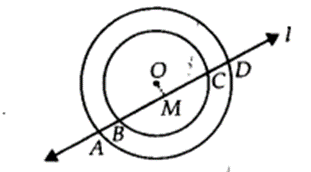
For the inner circle,
OM ⊥ l [By construction]
∴ BM = MC …(ii)
[Perpendicular from the centre to the chord bisects the chord]
Subtracting (ii) from (i), we have
AM – BM = MD – MC
⇒ AB = CD
Ex 10.4 Class 9 Maths Question 5.
Three girls Reshma, Salma and Mandip are playing a game by standing on a circle of radius 5m drawn in a park. Reshma throws a ball to Salma, Salma to Mandip, Mandip to Reshma. If the distance between Reshma and Salma and between Salma and Mandip is 6 m each, what is the distance between Reshma and Mandip?
Solution:
Let the three girls Reshma, Salma and Mandip be positioned at R, S and M respectively on the circle with centre O and radius 5 m such that
RS = SM = 6 m [Given]
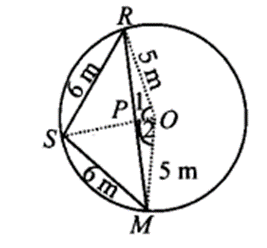
Equal chords of a circle subtend equal angles at the centre.
∴ ∠1 = ∠2
In ∆POR and ∆POM, we have
OP = OP [Common]
OR = OM [Radii of the same circle]
∠1 = ∠2 [Proved above]
∴ ∆POR ≅ ∆POM [By SAS congruence criteria]
∴ PR = PM and
∠OPR = ∠OPM [C.P.C.T.]
∵∠OPR + ∠OPM = 180° [Linear pair]
∴∠OPR = ∠OPM = 90°
⇒ OP ⊥ RM
Now, in ∆RSP and ∆MSP, we have
RS = MS [Each 6 cm]
SP = SP [Common]
PR = PM [Proved above]
∴ ∆RSP ≅ ∆MSP [By SSS congruence criteria]
⇒ ∠RPS = ∠MPS [C.P.C.T.]
But ∠RPS + ∠MPS = 180° [Linear pair]
⇒ ∠RPS = ∠MPS = 90°
SP passes through O.
Let OP = x m
∴ SP = (5 – x)m
Now, in right ∆OPR, we have
x2 + RP2 = 52
RP2 = 52 – x2
In right ∆SPR, we have
(5 – x)2 + RP2 = 62
⇒ RP2 = 62 – (5 – x)2 ……..(ii)
From (i) and (ii), we get
⇒ 52 – x2 = 62 – (5 – x)2
⇒ 25 – x2 = 36 – [25 – 10x + x2]
⇒ – 10x + 14 = 0
⇒ 10x = 14 ⇒ x = 1410 = 1.4
Now, RP2 = 52 – x2
⇒ RP2 = 25 – (1.4)2
⇒ RP2 = 25 – 1.96 = 23.04
∴ RP = 23.04−−−−√= 4.8
∴ RM = 2RP = 2 x 4.8 = 9.6
Thus, distance between Reshma and Mandip is 9.6 m.
Ex 10.4 Class 9 Maths Question 6.
A circular park of radius 20 m is situated in a colony. Three boys Ankur, Syed and David are sitting at equal distance on its boundary each having a toy telephone in his hands to talk each other. Find the length of the string of each phone.
Solution:
Let Ankur, Syed and David are sitting at A, S and D respectively in the circular park with centre O such that AS = SD = DA
i. e., ∆ASD is an equilateral triangle.
Let the length of each side of the equilateral triangle be 2x.
Draw AM ⊥ SD.
Since ∆ASD is an equilateral triangle.
∴ AM passes through O.
⇒ SM = 12 SD = 12 (2x)
⇒ SM = x
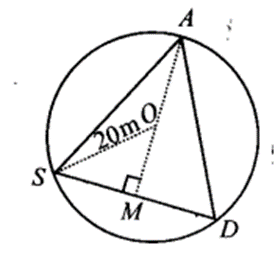
Now, in right ∆ASM, we have
AM2 + SM2 = AS2 [Using Pythagoras theorem]
⇒ AM2= AS2 – SM2= (2x)2 – x2
= 4x2 – x2 = 3x2
⇒ AM = 3x−−√m
Now, OM = AM – OA= (3x−−√ – 20)m
Again, in right ∆OSM, we have
OS2 = SM2 + OM2 [using Pythagoras theorem]
202 = x2 + (3x−−√ – 20)2
⇒ 400 = x2 + 3x2 – 403x−−√ + 400
⇒ 4x2 = 40 3x−−√
⇒ x = 10√3 m
Now, SD = 2x = 2 x 10√3 m = 20√3 m
Thus, the length of the string of each phone = 20√3 m
Ex 10.5 Class 9 Maths Question 1.
In figure A,B and C are three points on a circle with centre 0 such that ∠BOC = 30° and ∠ AOB = 60°. If D is a point on the circle other than the arc ABC, find ∠ ADC.
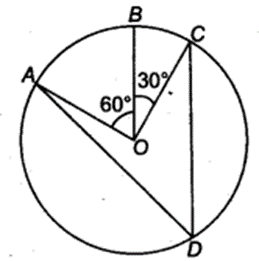
Solution:
We have a circle with centre O, such that
∠AOB = 60° and ∠BOC = 30°
∵∠AOB + ∠BOC = ∠AOC
∴ ∠AOC = 60° + 30° = 90°
The angle subtended by an arc at the circle is half the angle subtended by it at the centre.
∴ ∠ ADC = 12 (∠AOC) = 12(90°) = 45°
Ex 10.5 Class 9 Maths Question 2.
A chord of a circle is equal to the radius of the circle, find the angle subtended by the chord at a point on the minor arc and also at a point on the major arc.
Solution:
We have a circle having a chord AB equal to radius of the circle.
∴ AO = BO = AB
⇒ ∆AOB is an equilateral triangle.
Since, each angle of an equilateral triangle is 60°.
⇒ ∠AOB = 60°
Since, the arc ACB makes reflex ∠AOB = 360° – 60° = 300° at the centre of the circle and ∠ACB at a point on the minor arc of the circle.
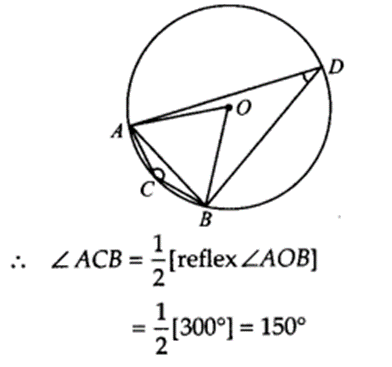
Hence, the angle subtended by the chord on the minor arc = 150°.
Similarly, ∠ADB = 12 [∠AOB] = 12 x 60° = 30°
Hence, the angle subtended by the chord on the major arc = 30°
Ex 10.5 Class 9 Maths Question 3.
In figure, ∠PQR = 100°, where P, Q and R are points on a circle with centre O. Find ∠OPR.
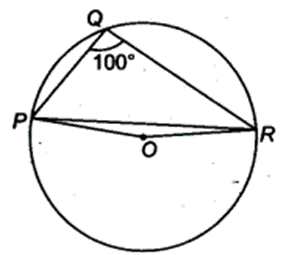
Solution:
The angle subtended by an arc of a circle at its centre is twice the angle subtended by the same arc at a point pn the circumference.
∴ reflex ∠POR = 2∠PQR
But ∠PQR = 100°
∴ reflex ∠POR = 2 x 100° = 200°
Since, ∠POR + reflex ∠POR = 360°
⇒ ∠POR = 360° – 200°
⇒ ∠POR = 160°
Since, OP = OR [Radii of the same circle]
∴ In ∆POR, ∠OPR = ∠ORP
[Angles opposite to equal sides of a triangle are equal]
Also, ∠OPR + ∠ORP + ∠POR = 180°
[Sum of the angles of a triangle is 180°]
⇒ ∠OPR + ∠ORP + 160° = 180°
⇒ 2∠OPR = 180° -160° = 20° [∠OPR = ∠ORP]
⇒ ∠OPR = 20∘2 = 10°
Ex 10.5 Class 9 Maths Question 4.
In figure, ∠ABC = 69°,∠ACB = 31°, find ∠BDC.
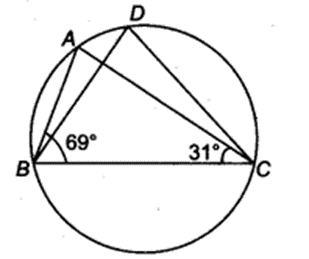
Solution:
In ∆ABC, ∠ABC + ∠ACB + ∠BAC = 180°
⇒ 69° + 31° + ∠BAC = 180°
⇒ ∠BAC = 180° – 100° = 80°
Since, angles in the same segment are equal.
∴∠BDC = ∠BAC ⇒ ∠BDC = 80°
Ex 10.5 Class 9 Maths Question 5.
In figure, A, B and C are four points on a circle. AC and BD intersect at a point E such that ∠ BEC = 130° and ∠ ECD = 20°. Find ∠BAC.
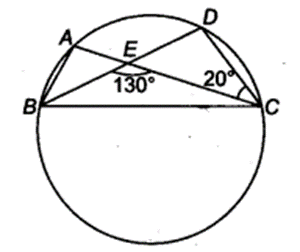
Solution:
∠BEC = ∠EDC + ∠ECD
[Sum of interior opposite angles is equal to exterior angle]
⇒ 130° = ∠EDC + 20°
⇒ ∠EDC = 130° – 20° = 110°
⇒ ∠BDC = 110°
Since, angles in the same segment are equal.
∴ ∠BAC = ∠BDC
⇒ ∠BAC = 110°
Ex 10.5 Class 9 Maths Question 6.
ABCD is a cyclic quadrilateral whose diagonals intersect at a point E. If ∠DBC = 70°, ∠BAC is 30°, find ∠BCD. Further, if AB = BC, find ∠ECD.
Solution:
Since angles in the same segment of a circle are equal.
∴ ∠BAC = ∠BDC
⇒ ∠BDC = 30°
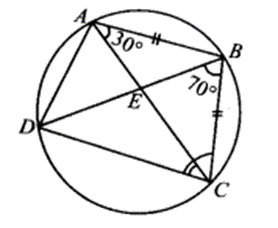
lso, ∠DBC = 70° [Given]
In ∆BCD, we have
∠BCD + ∠DBC + ∠CDB = 180° [Sum of angles of a triangle is 180°]
⇒ ∠BCD + 70° + 30° = 180°
⇒ ∠BCD = 180° -100° = 80°
Now, in ∆ABC,
AB = BC [Given]
∴ ∠BCA = ∠BAC [Angles opposite to equal sides of a triangle are equal]
⇒ ∠BCA = 30° [∵ ∠B AC = 30°]
Now, ∠BCA + ∠BCD = ∠BCD
⇒ 30° + ∠ECD = 80°
⇒ ∠BCD = 80° – 30° = 50°
Ex 10.5 Class 9 Maths Question 7.
If diagonals of a cyclic quadrilateral are diameters of the circle through the vertices of the quadrilateral, prove that it is a rectangle.
Solution:
Since AC and BD are diameters.
⇒ AC = BD …(i) [All diameters of a circle are equal]
Also, ∠BAD = 90° [Angle formed in a semicircle is 90°]
Similarly, ∠ABC = 90°, ∠BCD = 90°
and ∠CDA = 90°
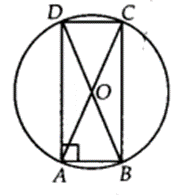
Now, in ∆ABC and ∆BAD, we have
AC = BD [From (i)]
AB = BA [Common hypotenuse]
∠ABC = ∠BAD [Each equal to 90°]
∴ ∆ABC ≅ ∆BAD [By RHS congruence criteria]
⇒ BC = AD [C.P.C.T.]
Similarly, AB = DC
Thus, the cyclic quadrilateral ABCD is such that its opposite sides are equal and each of its angle is a right angle.
∴ ABCD is a rectangle.
Ex 10.5 Class 9 Maths Question 8.
If the non – parallel sides of a trapezium are equal, prove that it is cyclic.
Solution:
We have a trapezium ABCD such that AB ॥ CD and AD = BC.
Let us draw BE ॥ AD such that ABED is a parallelogram.
∵ The opposite angles and opposite sides of a parallelogram are equal.
∴ ∠BAD = ∠BED …(i)
and AD = BE …(ii)
But AD = BC [Given] …(iii)
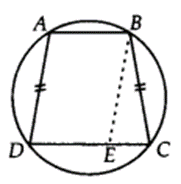
∴ From (ii) and (iii), we have BE = BC
⇒ ∠BCE = ∠BEC … (iv) [Angles opposite to equal sides of a triangle are equal]
Now, ∠BED + ∠BEC = 180° [Linear pair]
⇒ ∠BAD + ∠BCE = 180° [Using (i) and (iv)]
i.e., A pair of opposite angles of a quadrilateral ABCD is 180°.
∴ ABCD is cyclic.
⇒ The trapezium ABCD is cyclic.
Ex 10.5 Class 9 Maths Question 9.
Two circles intersect at two points B and C. Through B, two line segments ABD and PBQ are drawn to intersect the circles at A,D and P, Q respectively (see figure). Prove that ∠ ACP = ∠QCD.
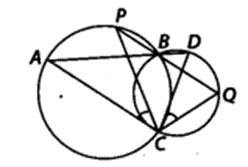
Solution:
Since, angles in the same segment of a circle are equal.
∴ ∠ACP = ∠ABP …(i)
Similarly, ∠QCD = ∠QBD …(ii)
Since, ∠ABP = ∠QBD …(iii) [Vertically opposite angles]
∴ From (i), (ii) and (iii), we have
∠ACP = ∠QCD
Ex 10.5 Class 9 Maths Question 10.
If circles are drawn taking two sides of a triangle as diameters, prove that the point of intersection of these circles lie on the third side.
Solution:
We have ∆ABC, and two circles described with diameter as AB and AC respectively. They intersect at a point D, other than A.
Let us join A and D.
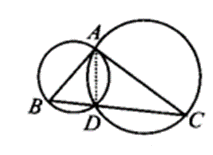
∵ AB is a diameter.
∴∠ADB is an angle formed in a semicircle.
⇒ ∠ADB = 90° ……(i)
Similarly, ∠ADC = 90° ….(ii)
Adding (i) and (ii), we have
∠ADB + ∠ADC = 90° + 90° = 180°
i. e., B, D and C are collinear points.
⇒ BC is a straight line. Thus, D lies on BC.
Ex 10.5 Class 9 Maths Question 11.
ABC and ADC are two right angled triangles with common hypotenuse AC. Prove that ∠CAD = ∠CBD.
Solution:
We have ∆ABC and ∆ADC such that they are having AC as their common hypotenuse and ∠ADC = 90° = ∠ABC
∴ Both the triangles are in semi-circle. Case – I: If both the triangles are in the same semi-circle.
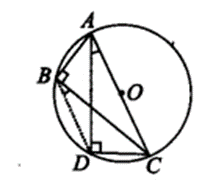
⇒ A, B, C and D are concyclic.
Join BD.
DC is a chord.
∴ ∠CAD and ∠CBD are formed in the same segment.
⇒ ∠CAD = ∠CBD Case – II : If both the triangles are not in the same semi-circle.
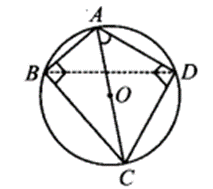
⇒ A,B,C and D are concyclic. Join BD. DC is a chord.
∴ ∠CAD and ∠CBD are formed in the same segment.
⇒ ∠CAD = ∠CBD
Ex 10.5 Class 9 Maths Question 12.
Prove that a cyclic parallelogram is a rectangle.
Solution:
We have a cyclic parallelogram ABCD. Since, ABCD is a cyclic quadrilateral.
∴ Sum of its opposite angles is 180°.
⇒ ∠A + ∠C = 180° …(i)
But ∠A = ∠C …(ii)
[Opposite angles of a parallelogram are equal]
From (i) and (ii), we have
∠A = ∠C = 90°
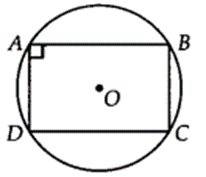
Similarly,
∠B = ∠D = 90°
⇒ Each angle of the parallelogram ABCD is 90°.
Thus, ABCD is a rectangle.
Ex 10.6 Class 9 Maths Question 1.
Prove that the line of centres of two intersecting circles subtends equal angles at the two points of intersection.
Solution:
Given : Two circles with centres O and O’ respectively such that they intersect each other at P and Q.
To Prove: ∠OPO’ = ∠OQO’.
Construction : Join OP, O’P, OQ, O’Q and OO’.
Proof: In ∆OPO’ and ∆OQO’, we have
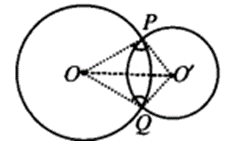
OP = OQ [Radii of the same circle]
O’P = O’Q [Radii of the same circle]
OO’ = OO’ [Common]
∴ AOPO’ = AOQO’ [By SSS congruence criteria]
⇒ ∠OPO’ = ∠OQO’ [C.P.C.T.]
Ex 10.6 Class 9 Maths Question 2.
Two chords AB and CD of lengths 5 cm and 11 cm, respectively of a circle are parallel to each other and are on opposite sides of its centre. If the distance between AB and CD is 6 cm, find the radius of the circle.
Solution:
We have a circle with centre O.
AB || CD and the perpendicular distance between AB and CD is 6 cm and AB = 5 cm, CD = 11 cm.
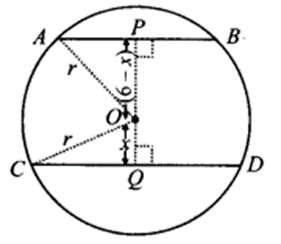
Let r cm be the radius of the circle.
Let us draw OP ⊥ AB and OQ ⊥ CD such that
PQ = 6 cm
Join OA and OC.
Let OQ = x cm
∴ OP = (6 – x) cm
∵ The perpendicular drawn from the centre of a circle to chord bisects the chord.
Ex 10.6 Class 9 Maths Question 3.
The lengths of two parallel chords of a circle are 6 cm and 8 cm. If the smaller chord is at distance 4 cm from the centre, what is the distance of the other chord from the centre ?
Solution:
We have a circle with centre O. Parallel chords AB and CD are such that the smaller chord is 4 cm away from the centre.
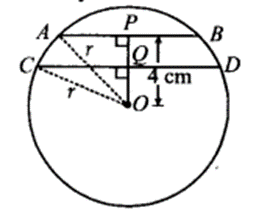
Let r cm be the radius of the circle and draw OP ⊥ AB and join OA and OC.
∵ OP ⊥ AB
∴ P is the mid-point of AB.
⇒ AP = 12AB = 12(6cm) = 3 cm
Similarly, CQ = 12CD = 12(8cm)= 4 cm
Now in ∆OPA, we have OA2 = OP2 + AP2
⇒ r2 = 42 + 32
⇒ r2 = 16 + 9 = 25
⇒ r = 25−−√ =5
Again, in ∆CQO, we have OC2 = OQ2 + CQ2
⇒ r2 = OQ2 + 42
⇒ OQ2 = r2 – 42
⇒ OQ2 = 52 – 42 = 25 – 16 = 9 [∵ r = 5]
⇒ OQ
⇒ √9 = 3
The distance of the other chord (CD) from the centre is 3 cm.
Note: In case if we take the two parallel chords on either side of the centre, then
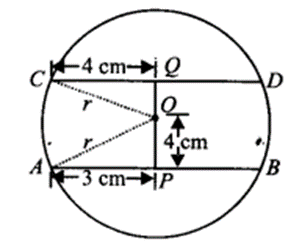
In ∆POA, OA2 = OP2 + PA2
⇒ r2 = 42 + 32 = 52
⇒ r = 5
In ∆QOC, OC2 = CQ2 + OQ2
⇒ OQ2 = 42 + OQ2
⇒ OQ2 = 52 – 42 = 9
⇒ OQ = 3
Ex 10.6 Class 9 Maths Question 4.
Let the vertex of an angle ABC be located outside a circle and let the sides of the angle intersect equal chords AD and CE with the circle. Prove that ∠ABC is equal to half the difference of the angles subtended by the chords AC and DE at the centre.
Solution:
Given : ∠ABC is such that when we produce arms BA and BC, they make two equal chords AD and CE.
To prove: ∠ABC = 12 [∠DOE – ∠AOC]
Construction: Join AE.
Proof: An exterior angle of a triangle is equal to the sum of interior opposite angles.
∴ In ∆BAE, we have
∠DAE = ∠ABC + ∠AEC ……(i)
The chord DE subtends ∠DOE at the centre and ∠DAE in the remaining part of the circle.
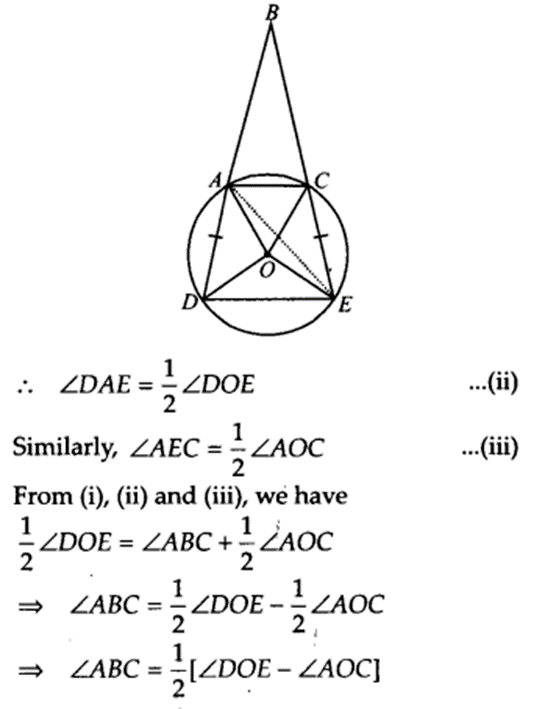
⇒ ∠ABC = 12 [(Angle subtended by the chord DE at the centre) – (Angle subtended by the chord AC at the centre)]
⇒ ∠ABC = 12 [Difference of the angles subtended by the chords DE and AC at the centre]
Download Mennta App and get access to free video lectures and hand crafted notes.