Chapter 9 – Algebraic Expressions and Identities Exercise 9.3
Ex 9.3 Class 8 Maths Question 1.
Carry out the multiplication of the expressions in each of the following pairs:
(i) 4p, q + r
(ii) ab, a – b
(iii) a + b, 7a2b2
(iv) a2 – 9, 4a
(v) pq + qr + rp, 0
Solution:
(i) 4p × (q + r) = (4p × q) + (4p × r) = 4pq + 4pr
(ii) ab, a – b = ab × (a – b) = (ab × a) – (ab × b) = a2b – ab2
(iii) (a + b) × 7a2b2 = (a × 7a2b2) + (b × 7a2b2) = 7a3b2 + 7a2b3
(iv) (a2 – 9) × 4a = (a2 × 4a) – (9 × 4a) = 4a3 – 36a
(v) (pq + qr + rp) × 0 = 0
[∵ Any number multiplied by 0 is = 0]
Ex 9.3 Class 8 Maths Question 2.
Complete the table.
| S.No. | First Expression | Second Expression | Product |
| (i) | a | b + c + d | – |
| (ii) | x + y – 5 | 5xy | – |
| (iii) | p | 6p2 – 7p + 5 | – |
| (iv) | 4p2q2 | p2 – q2 | – |
| (v) | a + b + c | abc | – |
Solution:
(i) a × (b + c + d) = (a × b) + (a × c) + (a × d) = ab + ac + ad
(ii) (x + y – 5) (5xy) = (x × 5xy) + (y × 5xy) – (5 × 5xy) = 5x2y + 5xy2 – 25xy
(iii) p × (6p2 – 7p + 5) = (p × 6p2) – (p × 7p) + (p × 5) = 6p3 – 7p2 + 5p
(iv) 4p2q2 × (p2 – q2) = 4p2q2 × p2 – 4p2q2 × q2 = 4p4q2 – 4p2q4
(v) (a + b + c) × (abc) = (a × abc) + (b × abc) + (c × abc) = a2bc + ab2c + abc2
Completed Table:
| S.No. | First Expression | Second Expression | Product |
| (i) | a | b + c + d | ab + ac + ad |
| (ii) | x + y – 5 | 5xy | 5x2y + 5xy2 – 25xy |
| (iii) | p | 6p2 – 7p + 5 | 6p3 – 7p2 + 5p |
| (iv) | 4p2q2 | p2 – q2 | 4p4q2 – 4p2q4 |
| (v) | a + b + c | abc | a2bc + ab2c + abc2 |
Ex 9.3 Class 8 Maths Question 3.
Find the products.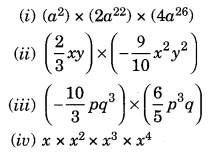
Solution: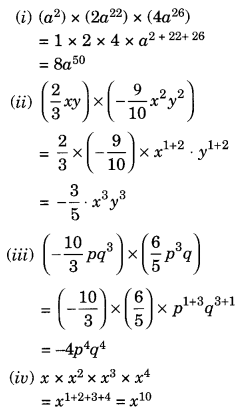
Ex 9.3 Class 8 Maths Question 4.
(a) Simplify: 3x(4x – 5) + 3 and find its values for (i) x = 3 (ii) x = 12.
(b) Simplify: a(a2 + a + 1) + 5 and find its value for (i) a = 0 (ii) a = 1 (iii) a = -1
Solution:
(a) We have 3x(4x – 5) + 3 = 4x × 3x – 5 × 3x + 3 = 12x2 – 15x + 3
(i) For x = 3, we have
12 × (3)2 – 15 × 3 + 3 = 12 × 9 – 45 + 3 = 108 – 42 = 66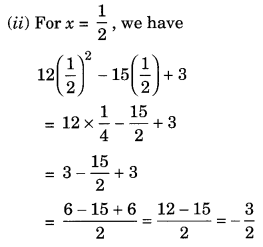
(b) We have a(a2 + a + 1) + 5
= (a2 × a) + (a × a) + (1 × a) + 5
= a3 + a2 + a + 5
(i) For a = 0, we have
= (0)3 + (0)2 + (0) + 5 = 5
(ii) For a = 1, we have
= (1)3 + (1)2 + (1) + 5 = 1 + 1 + 1 + 5 = 8
(iii) For a = -1, we have
= (-1)3 + (-1)2 + (-1) + 5 = -1 + 1 – 1 + 5 = 4
Ex 9.3 Class 8 Maths Question 5.
(a) Add: p(p – q), q(q – r) and r(r – p)
(b) Add: 2x(z – x – y) and 2y(z – y – x)
(c) Subtract: 3l(l – 4m + 5n) from 4l(10n – 3m + 2l)
(d) Subtract: 3a(a + b + c) – 2b(a – b + c) from 4c(-a + b + c)
Solution:
(a) p(p – q) + q(q – r) + r(r – p)
= (p × p) – (p × q) + (q × q) – (q × r) + (r × r) – (r × p)
= p2 – pq + q2 – qr + r2 – rp
= p2 + q2 + r2 – pq – qr – rp
(b) 2x(z – x – y) + 2y(z – y – x)
= (2x × z) – (2x × x) – (2x × y) + (2y × z) – (2y × y) – (2y × x)
= 2xz – 2x2 – 2xy + 2yz – 2y2 – 2xy
= -2x2 – 2y2 + 2xz + 2yz – 4xy
= -2x2 – 2y2 – 4xy + 2yz + 2xz
(c) 4l(10n – 3m + 2l) – 3l(l – 4m + 5n)
= (4l × 10n) – (4l × 3m) + (4l × 2l) – (3l × l) – (3l × -4m) – (3l × 5n)
= 40ln – 12lm + 8l2 – 3l2 + 12lm – 15ln
= (40ln – 15ln) + (-12lm + 12lm) + (8l2 – 3l2)
= 25ln + 0 + 5l2
= 25ln + 5l2
= 5l2 + 25ln
(d) [4c(-a + b + c)] – [3a(a + b + c) – 2b(a – b + c)]
= (-4ac + 4bc + 4c2) – (3a2 + 3ab + 3ac – 2ab + 2b2 – 2bc)
= -4ac + 4bc + 4c2 – 3a2 – 3ab – 3ac + 2ab – 2b2 + 2bc
= -3a2 – 2b2 + 4c2 – ab + 6bc – 7ac





Download Mennta App and get access to free video lectures and hand crafted notes.